Cubo di un binomio
Thursday, September 24th, 2009I passaggi per risolvere il cubo di un binomio.
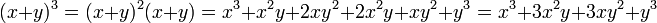

Immagini via Wikipedia
I passaggi per risolvere il cubo di un binomio.
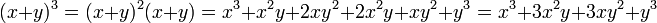

Immagini via Wikipedia
Ecco 2 casi particolari di disequazioni con valore assoluto:
|f(x)| < k
Si risolve con questo sistema
f(x) < k
f(x) > -k
|f(x)| > k
Si risolve con questo sistema
f(x) < -k U f(x) > k
Vedi come fare le disequazioni con modulo qui.
L’operazione di valore assoluto è univoca, cioè agisce su un’unica quantità. Tale operazione lascia invariato il segno delle quantità positive e non agisce sulle quantità nulle. Mentre cambia il segno delle quantità negative per renderle positive.
|+3| = +3
|-3| = +3
Se all’interno dei un valore assoluto è presente una quantità variabile (x) devo prima studiare il segno per capire quando lasciarla invariata e quando cambiarla di segno.
Quindi ogni quantità in modulo deve essere “sciolta”, cioè suddivisa in 2 o più sottocasi dopo aver studiato il segno dell’argomento del modulo.
| f(x) | < g(x)
M: | f(x) | >= 0
Provando con i numeri
|5x – 6| – x < 7
M: |5x -6| >= 0 (all’interno ci può assere anche una quantità nulla) ;
M: x >= 6/5
Se facciamo il grafico dei segni ricaviamo che da 6/5 in poi è positivo e dall’altra parte è negativo. Facciamo 2 sistemi, uno per ogni caso.
Caso 1: (troviamo le soluzioni positive)
x >= 6/5
5x – 6 -x < 7
Caso 2: (troviamo le soluzioni negative)
x < 6/5
- ( 5x – 6 ) -x < 7 (e continuare)
Unire poi le soluzioni. In questo caso – 1/6 < x < 13/4
Una disequazione si dice irrazionale quando presenta l’incognita sotto il segno della radice.
Se l’indice della radice è dispari:
√f(x) + y > 2
√f(x) > 2 – y
f(x) > (2 – y)² (…)
Se l’indice della radice è pari abbiamo due tipologie:
Per risolvere A:
Impostato a sistema
f(x) >= 0 (affinchè ciò che è sotto radice sia maggiore uguale a zero)
g(x) < 0 (tutte le soluzioni con g(x) minore di zero)
Unito a
g(x) >= 0 (per trovare tutte le sue soluzioni >= 0)
f(x) > [g(x)]² (elevando entrami alla seconda affinchè f(x) sia maggiore di g(x) )
Per risolvere B:
Impostato a sistema
f(x) >= 0
g(x) > 0
f(x) < [g(2)]²
Non inseriamo anche g(x) < 0 rispetto a prima perchè √f(x) è sempre maggiore o uguale a zero.
Si ricordi che ogni radice con radicando nullo (√0) da risultato nullo (0).